[最も人気のある！] factorise x^2-y^2/100 227536

How to factor expressions If you are factoring a quadratic like x^25x4 you want to find two numbers that Add up to 5 Multiply together to get 4 Since 1 and 4 add up to 5 and multiply together to get 4, we can factor it like (x1) (x4)Try typing these expressions into the calculator, click the blue arrow, and select "Factor" to see a demonstration Or, use these as a template to create and solve your own problems Problem 4x2 −9 4 x 2 − 9 Solution (2x3)(2x −3) ( 2 x 3) ( 2 x − 3) Problem x4 −81 x 4 − 81 Solution Using formula, (x y z) 2 = x 2 y 2 z 2 2xy 2yz 2zx Then, x 2 y 2 z 2 2xy 2yz 2zx = (x y z) 2 4x 2 9y 2 16z 2 12xy – 24yz – 16xz = (2x) 2 (3y) 2 (−4z)2 (2 × 2x × 3y) (2 × 3y × −4z) (2 × −4z × 2x) = (2x 3y – 4z) 2 = (2x 3y – 4z) (2x 3y – 4z) (ii) 2x 2 y 2 8z 2 – 2√2xy 4√2yz – 8xz Solution Using

7th Pages 101 114 Flip Pdf Download Fliphtml5

Factorise x^2-y^2/100

Factorise x^2-y^2/100-Factoring » Tips for entering queries Enter your queries using plain English To avoid ambiguous queries, make sure to use parentheses where necessary Here are some examples illustrating how to ask about factoring factor quadratic x^27x12;Expand polynomial (x3)(x^35x2) GCD of x^42x^39x^246x16 with x^48x^325x^246x16

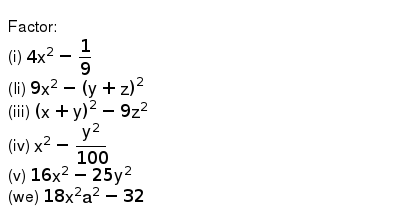
ग णनखण ड क ज ए I 4x 2 1 9 Ii 9x 2 Y Z 2 Iii X Y 2 9z 2 Iv X 2 Y 2 100 V 16x 2 25y 2 Vi 18x 2 A 2 32

17 Factorisation (EMAG) Factorisation is the opposite process of expanding brackets For example, expanding brackets would require \ (2 (x 1)\) to be written as \ (2x 2\) Factorisation would be to start with \ (2x 2\) and end up with \ (2 (x 1)\) The two expressions \ (2 (x 1)\) and \ (2x2\) are equivalent;Example 4 Factor 49 x 2 − 100 y 2 Solution Here we have a binomial with two variables and recognize that it is a difference of squares Therefore, a = 7 x and b = 10 y Substitute into the formula for difference of squares CHAPTER 7 FACTORISING ALGEBRAIC EXPRESSIONS 177 Factorise the following completely a 5x 15 y b −3m − m2 c 6xy − 2 x d 15 p − q e 15 pq − q f 12 st 2 15 st g −18 xy − 6 x h at − at 2 i 7x2y xy j a2 ab Factorise each of the following a a2 ab 3 a b xy − 3 x2 2 x c 12 st − 4 t3 8 t d 36 − 12 ab 18 b e 3ab − 9 a2b 12 ab 2 a2b2 f 4m − 8 n −

 In this case, our perfect squares are x2 and one hundred, so this can be factored out as (x 10)(x 10)Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us! This is known as a difference of squares It can be factored as x^2 y^2 = (xy)(xy) Notice that when you multiply (xy) by (xy) then the terms in xy cancel out, leaving x^2y^2 (xy)(xy) = x^2xyyxy^2 = x^2xyxyy^2 = x^2y^2 In general, if you spot something in the form a^2b^2 then it can be factored as (ab)(ab) For example 9x^216y^2 = (3x)^2(4y)^2

Since a^2b^2 = (ab) (ab), therefore100x^2 = (10x) (10x) Answered by Howard M • Maths tutor 9 Views See similar Maths GCSE tutorsFactorising an expression is to write it as a product of its factors There are 4 methods common factor, difference of two squares, trinomial/quadratic expression and completing the squareAccording to remainder theorem f (2) = 0 so that (x – 2 ) is a factor of x3 2x2 x 2 Here maximum power of x is 3 so that its can have maximum 3 factors So our answer is (x1) (x1) (x2) (ii) x3 3x2 9x 5 Possible zeros are factors of ± constant term / coefficient of leading term Here constant term is 5 and coefficient of

3 Factorise The Following Using Appropriate Identities N Begin Array L L L L Text I 9 X 2 6 X Y Y 2 Text Ii 4 Y 2 4 Y 1 Text Iii X 2 Frac Y 2 100

Ex 2 5 3 Factorise Following Using Appropriate Identities

Algebra Factor x^2100 x2 − 100 x 2 100 Rewrite 100 100 as 102 10 2 x2 − 102 x 2 10 2 Since both terms are perfect squares, factor using the difference of squares formula, a2 −b2 = (ab)(a−b) a 2 b 2 = ( a b) ( a b) where a = x a = x and b = 10 b = 10 (x10)(x −10) ( x 10) ( x Transcript Example 21 Factorize 4x2 y2 z2 – 4xy – 2yz 4xz 4x2 y2 z2 – 4xy – 2yz 4xz = 22 x2 y2 z2 – 4xy – 2yz 4xz = (2x)2 y2 z2The fundamental theorem of algebra tells us that all polynomials with complex coefficients can be factored completely over the complex numbers mathx^21/math is such a polynomial Feasibility is a separate question, with a happy answer for qu

What Is The X Intercept Of X 2x 5x 2 Quora

How Do You Factor Completely 81x 2 100 Socratic

They have the sameCompletely factor the following expression {eq}100x^2 160xy 64y^2 {/eq} Simplification It is a method where we deduce the simplest form from any given expressionWe think you wrote (4x)^2(3y)^2100 This deals with factoring multivariable polynomials

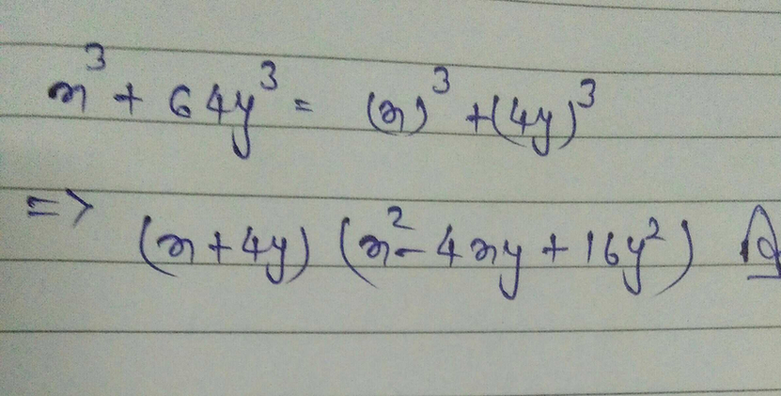
Factorise X 64y Scholr

7th Pages 101 114 Flip Pdf Download Fliphtml5

 Suppose that the functions s and t are defined for all real numbers x as follows s(x) x4 and t(x)=4x1 write the expressions for (s•t) and (x) and (st) and evaluate (st)(2) Algebra To which subset of real numbers does the following number belong?Expressions like 5xy, 7x 2 y, 2x(y3), 11(y1) (x2) are already in an irreducible factor form On the other hand in expressions like 6x8, 5x5y, x 2 7x, x 2 3x6 we need to determine factors, for which we develop systematic methods to factorise these expressions In the space below we will reduce various forms of algebraic expressions using11 Factoring y2100 Theory A difference of two perfect squares, B2 can be factored into (AB) • (AB) Proof (AB) • (AB) = AB BA B2 = AB AB B2 = B2 Note AB = BA is the commutative property of multiplication Note AB AB equals zero and is therefore eliminated from the expression

2

Factorize The Following Expression 9 A B 2 100 X Y 2

Complete Factor x^2y^2 Shell, There is a great deal of pattern recognition in factoring, by that I mean looking at an expression and seeing patterns you have seen before and recognizing how to factor them This is true of the "difference of squares" you sent us, x 2 y 2 Once you think you know the factors you can check by multiplication I wanted to post the factorisation of x^2 y^2 as a hint, because once that is factored, the rest is trivial Or so I thought Hint 2 There is another x y in the expression $\endgroup$ – gnasher729 Sep 7 '16 at 1518Selina solutions for Concise Mathematics Class 8 ICSE chapter 13 (Factorisation) include all questions with solution and detail explanation This will clear students doubts about any question and improve application skills while preparing for board exams The detailed, stepbystep solutions will help you understand the concepts better and clear your confusions, if any

Example 18 Factorize I 49a2 70ab 25b2 Ii 25 9

One Possible Equation Of The Chord Of X 2 Y 2 100 That Passes Through 1 7 And Subtends An Angle Frac 2 Pi 3 At Origin Is Begin Array Ll Text A 3 Y 4 X 25 0 Text

X y = G What can QuickMath do?Formula of polynomials If the polynomial k 2 x 3 − kx 2 3kx k is exactly divisible by (x3) then the positive value of k is ____Factoriser Factoriser Enter a quadratic equation to factorise For indices use (^) Factorise Submit

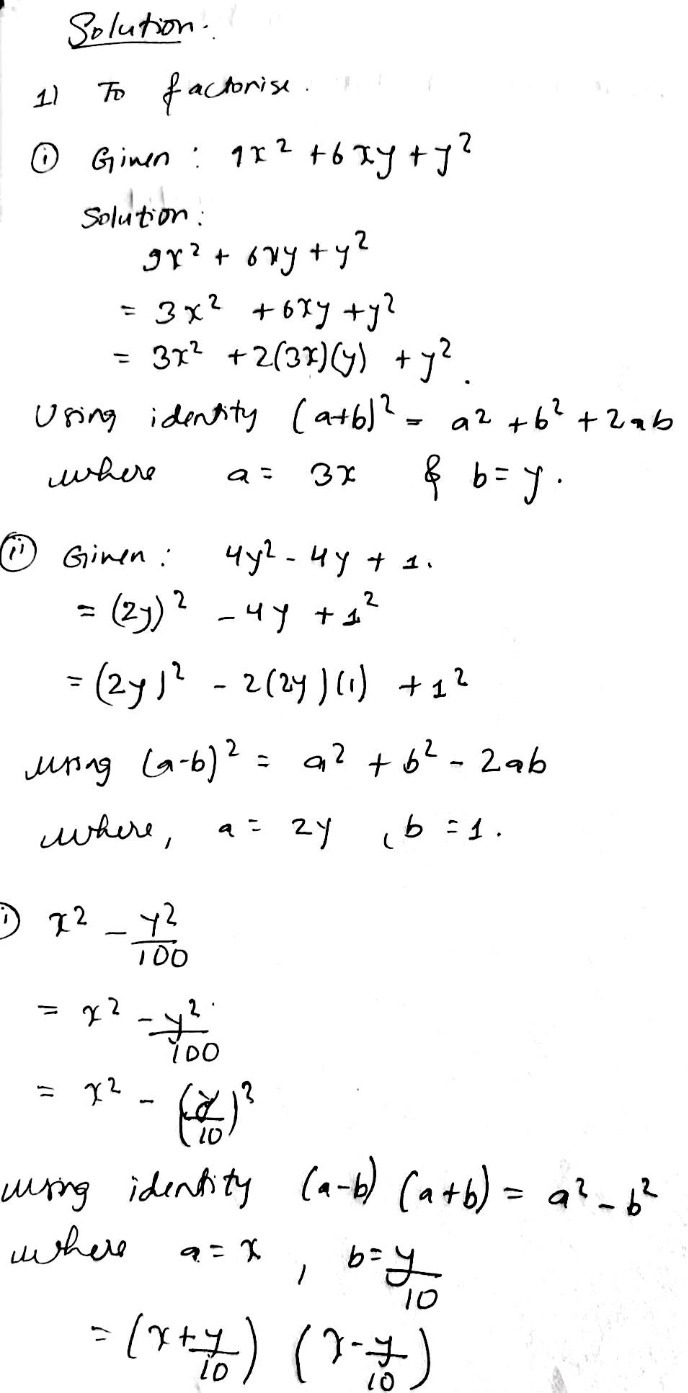
Factorise The Following Using Appropriate Identitics I 9x 2 6xy Y 2 Ii 4y 2 4y 1 Iii X 2 Frac Y 2 100 Snapsolve

Factorise X 2 x 100

Factorise x^2 y^2/100 # School Factorise x^2 y^2/100 Post Answer Answers (1) R Ravindra Pindel = x 2 y 2 /100 {a 2 b 2 = (ab) (ab) } = ( x y/10) (x y/10) Similar Questions Need Solution for RDSharma Maths Class 12 Chapter 3 Inverse Trigonomeric Functions Exercise 314 Question 11 Maths Textbook SolutionQuickMath will automatically answer the most common problems in algebra, equations and calculus faced by highschool and college students The algebra section allows you to expand, factor or simplify virtually any expression you choose It also has commands for splitting fractions into partial fractionsTo ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW Factorise `x^2xyxzyz`

Quadratic Equations Learning Outcomes Factorise By Use Of Difference Of Two Squares Factorise Quadratic Expressions Solve Quadratic Equations By Ppt Download

How To Factorise 100 X 5 2 Brainly In

Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!The factorized form of the following 9x 2 6xy y 2, 4y 2 4y 1, and x 2 y 2 /100 using appropriate identities are (3x y) 2, (2y 1) 2, and (x y/10) (x What must be subtracted from 4x^42x^36x^22x6 so that the result is exactly divisible by 2x^2x1?

Quadratic Functions And Inequalities Ppt Download

Factorise The Following Using Appropriate Identities I 9x 2 6xy Y 2 Ii 4y 2 4y 1 Iii X 2 Y 2 100

(x^2–4x)(x^2–4x1) Let (x^2–4x)=p = p(p1) = p^2 p = p^2 5p 4p = p (p5 ) 4 (p 5 ) = (p 5 ) (p 4 ) put p = x^2 4x = (x^2 4 Ex 25, 2 Evaluate the following products without multiplying directly (iii) 104 × 96 104 × 96 = (100 4) (100 − 4) Using the identity (x y) (x – y) = x2 – y2 where x = 100 , y = 4 = (100)2 − (4)2 = − 16 = 9984 Ex 25, 3 Factorise the following using appropr factorise x^2x100

Factorize 16 A 2 25 4a 2 Ii 16 A 2b B 16 A 2 100 X Y 2 81 A B 2 X 1 2 X 2 2

Factorize I X 2 Y 2 100 Ii 100 9x 2 Iii 49x 2 1 4

 Factor 5(x^3)(y^2)(z) 100(x^2)(y^3)(z^2) by factoring out their greatest common factor NOTE The parentheses have been added to distinguish terms from each other Factor as x^4 x^2 1 = (x^2 x 1)(x^2 x 1) To find this, first notice that x^4 x^2 1 > 0 for all (real) values of x So there are no linear factors, only quadratic ones x^4 x^2 1 = (ax^2 bx c)(dx^2 ex f) Without bothering to multiply this out fully just yet, notice that the coefficient of x^4 gives us ad = 1 We might as well let a = 1 and d = 1 = (x^2 bx c)(x^2Polynomial identities (short multiplication formulas) (x y) 2 = x 2 2xy y 2 (x y) 2 = x 2 2xy y 2 Example 1 If x = 10, y = 5a (10 5a) 2 = 10 2 2·10·5a (5a) 2 = 100 100a 25a 2 Example 2 if x = 10 and y is 4 (10 4) 2 = 10 2 2·10·4 4 2 = 100 80 16 = 36 The opposite is also true 25 a 4a 2 = 5 2

Factorize I X 2 Y 2 100 Ii 100 9x 2 Iii 49x 2 1 4

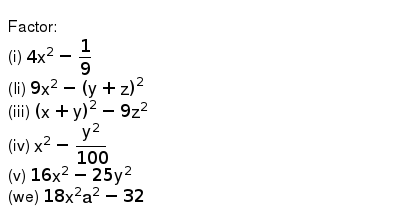
ग णनखण ड क ज ए I 4x 2 1 9 Ii 9x 2 Y Z 2 Iii X Y 2 9z 2 Iv X 2 Y 2 100 V 16x 2 25y 2 Vi 18x 2 A 2 32

Example Factor 6x^2 19x 10 6*10 = 60, so we need to find two numbers that add to 19 and multiply to give 60 These numbers (after some trial and error) are 15 and 4 So split up 19x into 15x 4x (or 4x 15x), then factor by grouping 6x^2 19x 10 = 6x^2 15x 4x 10 = 3x (2x 5) 2Class 8 Maths Chapter 14 Extra Questions Factorise (а) 14m 5 n 4 p 2 – 42m 7 n 3 p 7 – 70m 6 n 4 p 3 (b) 2a 2 (b 2 – c 2) b 2 (2c 2 – 2a 2) 2c 2 (a 2 – b 2) The area of a rectangle is 6a 2 36a and 36a width Find the length of the rectangle What are the common factors ofSquare root of 7 A)rational numbers B)irrational numbers****** C)whole numbers, integers

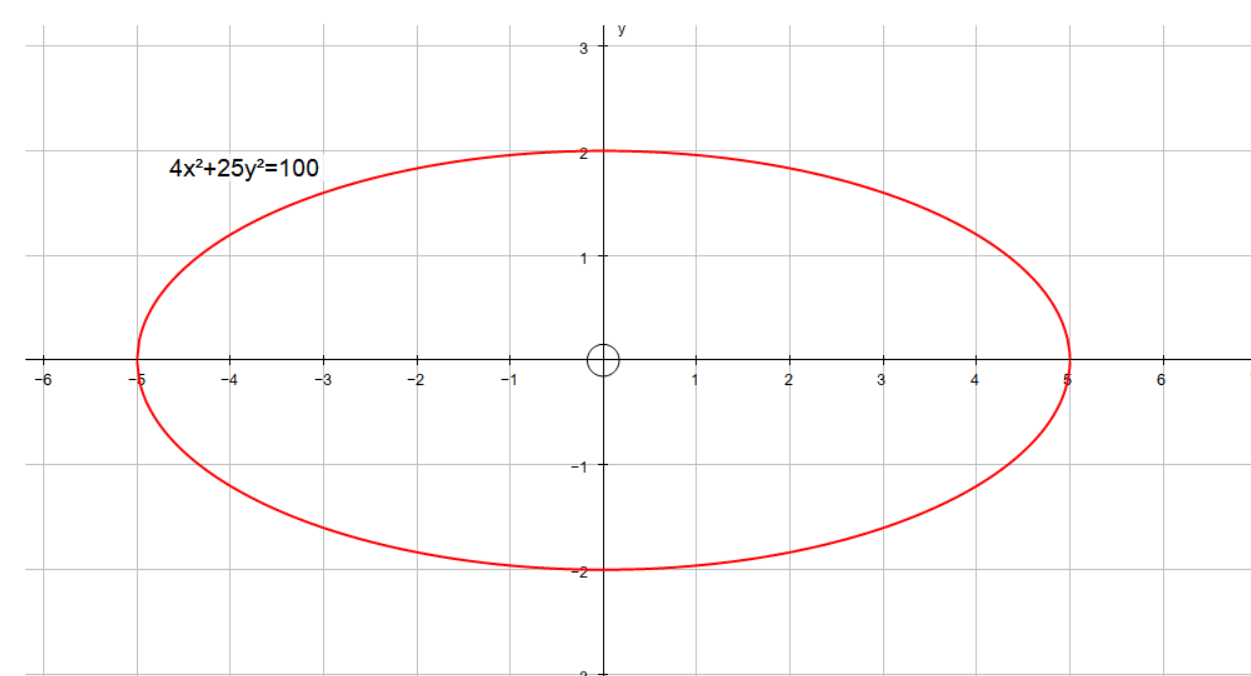
How Do You Find The Domain And Range Of 4x 2 25y 2 100 Algebraically Socratic

How To Factorise X 2 Y 2 2x 6y 8 Quora

Click here👆to get an answer to your question ️ Factorise the following using suitable identities x^2 y^2 2x 1Algebra Factor y^2100 y2 − 100 y 2 100 Rewrite 100 100 as 102 10 2 y2 − 102 y 2 10 2 Since both terms are perfect squares, factor using the difference of squares formula, a2 −b2 = (ab)(a−b) a 2 b 2 = ( a b) ( a b) where a = y a = y and b = 10 b = 10Solution Steps { x }^ { 2 } 3x2 x 2 − 3 x 2 Factor the expression by grouping First, the expression needs to be rewritten as x^ {2}axbx2 To find a and b, set up a system to be solved Factor the expression by grouping First, the expression needs to be rewritten as x 2 a x b x 2

Factorise X Y 2 7 X 2 Y 2 12 X Y 2 Youtube

Difference Of Two Squares Gcse Maths Examples Questions Worksheet

Factorise x^22xyy^2〖4z〗^2Factorise x2 2xy y2 4z2 Factorise (i) 4 x 2 9y 2 16z 2 12xy – 24yz – 16xz (ii) 2x 2 y 2 8z 2 – 2√2xy 4√2yz – 8xz Solution (102) 3 = (100 2) 3 = 100 3 2 3 3x 100x 2 (100 2 Using identity (x y) 3 = x 3 y 3 3xy (x y) = 8 600(100 2) = 8 10= (iii) (998) 3 = () 3 =1000 3 – 2 3 – 3xMATH Factoring Example 1 Completely factor x2 2xy ¡8y2 Solution x2 2xy ¡8y2 = (x¡2y)(x4y) Example 2 Completely factor x2y2 8xy 15 Solution x2y2 8xy 15 = (xy 3)(xy 5) Example 3 Completely factor 3x2 ¡12x¡36 Solution 3x2 ¡12x¡36 = 3(x2 ¡4x¡12) = 3(x2)(x¡6) The Sum/Difference of Two Squares

X 2 Y 2 Z 2 100 Xy Yz Zx 2 Brainly In

Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes

Factorise 100x^2 Via inspection, one can factorise this via the difference of squares;Add y^ {2} to both sides Add y2 to both sides x^ {2}=100y^ {2} x2 = 100 y2 Take the square root of both sides of the equation Take the square root of both sides of the equation x=\sqrt {y^ {2}100} x=\sqrt {y^ {2}100} x = y2 100Factorise (x^2100) and then solve for x When looking at factorising quadratic equations, the first approach should be to identify what is in front of the x term and the value of the c term, with the equation being in the form of y=A(x^2)BxcSo to factorise we first want to identify what B and C areWe then want to identify two numbers which

Which Identity Will Be Used To Factorise Y Square X Square Divided By 100 Brainly In

Factorise Each Of The Following Expression Y 2 y 100 Brainly In

And now solve the difference of two squares with a = 36 and b = 4y 2 Solution Factor the equation (rearranged) 36 − 4 y 2 using the identity a 2 − b 2 = ( a b) ( a − b) First factor out the GCF 4 ( 9 − y 2) Both terms are perfect squares so from a 2 b 2 we can find a and b

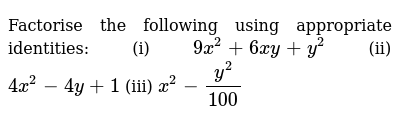
Factorise The Following Using Appropriate Identities I 9x 2 6x Y Y 2 Ii 4x 2 4y 1 Iii X 2 Y 2 100

Factorise X Y 100 Brainly In

Factorisation Class 8 Extra Questions Maths Chapter 14 Learn Cbse

Which Identity Do We Use To Factorise Tex X 2 Frac Y 2 100 Frac Xy 5 Tex A Tex A B 2 A 2 B 2 2ab Tex B Tex A B 2 A 2 B 2 2ab Tex C Tex A B C 2 A 2 B 2 C 2 2ab 2bc 2ca Tex D Tex A B C 2 A

Factorisation Class 8 Extra Questions Maths Chapter 14 Learn Cbse

Solved Factor X2 21x 100 Chegg Com

Factorization Of Polynomials Using Factor Theorem A Plus Topper

Quadratic Function 2 Www Mathsrevision Com Nat 5

Factor Factor A Polynomial And Trinomial With Step By Step Math Problem Solver

Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes

Factorise 100 X 5 2 Brainly In

The Unintegrated Parton Distributions F A X K T 2 M 2 At Scale M Download Scientific Diagram

X 2 Y 2 100 Factorise Using Appropriate Identities Youtube

Factorise 9 A B 2 100 X Y 2 Brainly In

How To Factorise X X 3x 4x 4 Completely Quora

Solving Quadratic Equations By Factoring Old Video Khan Academy

Factorize X 2 Y 2 100 Brainly In

Using A Suitable Identity Factorise The Following Expressions I X2 4 Y2 4 Ii X2 Y2 Brainly In

1

Class 9th Chapter 2 Ex 2 5 Q 3 Factorize Using Suitable Identities X 2 Y 2 100 Cbse Ncert Ytshorts Youtube

Ppt Solving Quadratic Equations Powerpoint Presentation Free Download Id

Olympic College Topic 12 Factorisation Topic 12 Factorisation 1 How To Find The Greatest Common Factors Of An Algebraic Expression Definition A Factor Ppt Download

100 X Y 2 81 A B 2 Brainly In

Q Tbn And9gcs3l3rkdzget 1gopdbixps8wfy Tywlb6lz L2gbhbl07zyv Usqp Cau

Factors Learning Outcomes Ppt Download

Factorise The Following Expressions Using Suitable Identities Tex A 100 9x 2 Tex Brainly In

Warmup Factor The Following Polynomials 1 7 X

Ncert Solutions For Class 9 Maths Chapter 2 Exercise 2 5 Polynomials

Factorise X Square Minus Y Square Upon 100 Brainly In

Telangana Scert Class 9 Math Solution Chapter 2 Polynomials And Factorisation Exercise 2 5

Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes

Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes

To I Dciuttuu On 14 Factorise 100 A B2 2ab Ar Implify Y 1 X 2 X2 9x 14

1

Ncert Solution 9 Math Chap 2 Polynomials Freeguru Helpline

Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes

2

Ex 2 5 3 Factorise Following Using Appropriate Identities

Math Factorize And Expand Easy To Understand

Factorise The Following Using Appropriate Identities I 9x 2 6xy Y 2 Ii 4y 2 4y 1 Iii X 2 Y 2 100 Sarthaks Econnect Largest Online Education Community

Factorisation Class 8 Extra Questions Maths Chapter 14 Learn Cbse

Factorise X 2 x 100 Brainly In

Factorize I 25x 2 Y 2 Ii 4 25x 2 Iii X Y 2 1

Factorize 9z Cube 27z Square 100z 300 If It Is Given That 3z 10 Is A Factor Of It Mathematics Topperlearning Com 9d7wgyyy

Example 18 Factorize I 49a2 70ab 25b2 Ii 25 9

Solve This Factorise The Following 1 X2 9y2 2 Maths Polynomials Meritnation Com

Factor 16x 2 100 Factor 16x Squared Minus 100

Factorise The Following Using Appropriate Identities I 9x 2 6x Y Y 2 Ii 4x 2 4y 1 Iii X 2 Y 2 100

Solutions Mr Barton Maths

Factorise The Following Using Appropriate Identities I 9x 2 6xy Y 2 Ii 4y 2 4y 1 Iii X 2 Y 2 100 Sarthaks Econnect Largest Online Education Community

Example 11 Using The Identity I Find I 2x 3y 2 Ii 103 2

Solution Can We Find The Two Circles That Satisfy These Three Conditions Circles Underground Mathematics

Factorise The Following Using Appropriate Identities I 9x 2 6x Y Y 2 Ii 4x 2 4y 1 Iii X 2 Y 2 100

X 2 Y 2 100

How To Factorise X Y 100 With Suitable Indentities Brainly In

Factorize X 2 Y 2 100 Maths Questions

X 2 Y 2 100

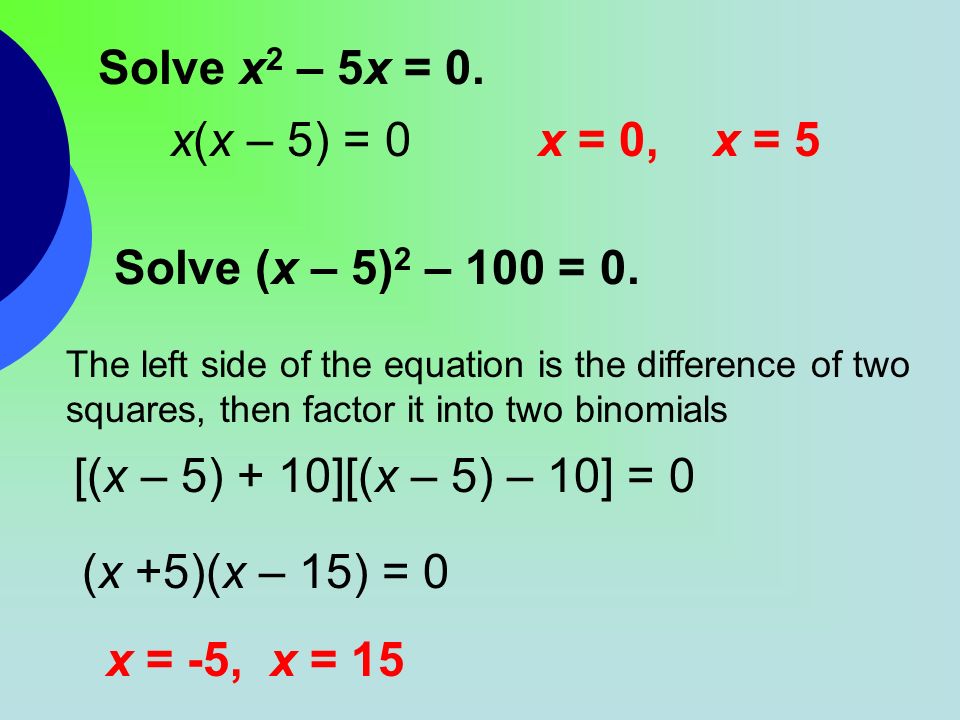
Aim How Do We Solve Quadratic Equations By Factoring Ppt Video Online Download

Q Tbn And9gcq2zdm1j6iaea7 Nv8rt1pmf37hdnswizud7h0yjdaecsm1r Dv Usqp Cau

3 Factorise Each Of The Following Expressions C Gauthmath

How To Solve X 2 x 100 0 By Factoring Youtube

Rd Sharma Solutions For Class 8 Chapter 7 Factorization Download Free Pdf

Telangana Scert Class 9 Math Solution Chapter 2 Polynomials And Factorisation Exercise 2 5

Example 1 Factor The Expression A M 2 25 B Q 2 625 C 9y 2 Ppt Download

Factorize I X 2 Y 2 100 Ii 100 9x 2 Iii 49x 2 1 4

Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes

7 05 Mb Solve X 8x 16 0 Download Lagu Mp3 Gratis Mp3 Dragon

3 Factorise Each Of The Following Expressions C Gauthmath

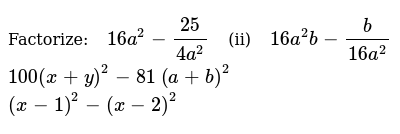
Factorize 16 A 2 25 4a 2 Ii 16 A 2b B 16 A 2 100 X Y 2 81 A B 2 X 1 2 X 2 2

Factor X 2 100 Youtube

Factorise The Following Using Appropriate Identities 9x2 6xy Y2 4y2 4y 1 X2 Y2 100 Youtube

X 2 Y 2 100

Quadratic Equations Learning Outcomes Factorise By Use Of Difference Of Two Squares Factorise Quadratic Expressions Solve Quadratic Equations By Ppt Download

Factorisation Mixed Knightswood Secondary School

Factorising Dops 8d Mathsccw

Solve Each Of The Following Quadratic Equations 4x 2 9x 100 Youtube